Non-Hermitian physics has been widely studied to understand the property of various open systems. Intriguing features including nonreciprocity, half-integer winding numbers, and non-Hermitian skin effect are demonstrated both in non-Hermitian solid-state systems and photonics. In recent years, the parity and time reversal (PT) symmetry has attracted broad interest in non-Hermitian systems, since system can undergo phase transition between PT-unbroken and PT-broken phases. Therefore, one can manipulate the topological properties of non-Hermitian systems through PT symmetry and achieve exotic phenomena such as topological phase transition and localized edge states. In photonics, PT symmetry is introduced by gain and loss that are distributed in a geometrically symmetric way.

In this work, we study a finite two-leg ladder model with on-site gain and loss on two legs respectively, and study the corresponding behaviors of localized states, which can be controlled by the amplitude of gain/loss. The non-Hermitian system is highly sensitive to boundary conditions, here we investigate the two-leg ladder model in the diagonal-edge open boundary condition (OBC). We find that, with small gain and loss, the system holds a pair of zero-energy modes with pure positive and negative imaginary eigenvalues that exhibit localized distributions at edges. When the gain and loss further increase, a phase transition happens and the localization features collapse. The eigen-modes of the lattice all extend into the bulk of the lattice. Moreover, the introduction of the effective magnetic flux can influence the localization effects.

Simulations results present phenomena consistent to the theoretical analysis, and interestingly, we show the existence of the gain mode localized at the edge. This work offers the opportunity for controlling the localized states in a finite system through the non-Hermiticity and shows potential application towards implementing high-power laser arrays in both real space and synthetic dimensions.

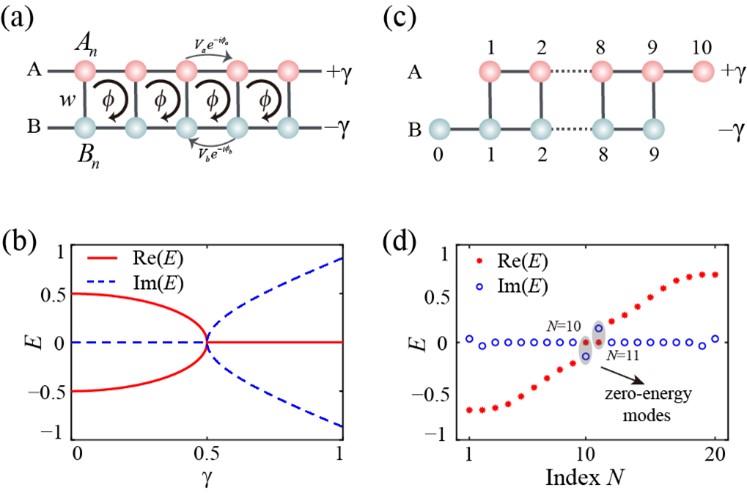
Figure (a) Schematic of a periodic two-leg ladder system. (b) The energy spectrum of the system in (a) as a function of the on-site gain and loss. (c) A finite two-leg ladder system with on-site gain and loss under the diagonal-edge boundary condition. (d) The eigenvalues of the lattice model in (c).

The research was published in “Rui Ye, Guangzhen Li, Luojia Wang, Xiaoxiong Wu, Luqi Yuan, and Xianfeng Chen, "Controlling localized states in a two-leg ladder lattice with diagonal edges via gain/loss [Invited]," Opt. Mater. Express 12, 4755-4767 (2022)”

Link: https://doi.org/10.1364/OME.477926